Ctrl+K

Applying Stochastic Methods

Applying Stochastic Methods#

Getting Started#

This tutorial focuses on using stochastic methods to estimate ultimates.

Be sure to make sure your packages are updated. For more info on how to update your pakages, visit Keeping Packages Updated.

# Black linter, optional
%load_ext lab_black

import pandas as pd
import numpy as np
import chainladder as cl
import matplotlib.pyplot as plt
import statsmodels.api as sm

print("pandas: " + pd.__version__)
print("numpy: " + np.__version__)
print("chainladder: " + cl.__version__)

pandas: 2.1.4
numpy: 1.24.3
chainladder: 0.8.18

Disclaimer#

Note that a lot of the examples shown might not be applicable in a real world scenario, and is only meant to demonstrate some of the functionalities included in the package. The user should always follow all applicable laws, the Code of Professional Conduct, applicable Actuarial Standards of Practice, and exercise their best actuarial judgement.

Intro to MackChainladder#

Like the basic Chainladder method, the MackChainladder is entirely specified by its selected development pattern. In fact, it is the basic Chainladder, but with extra features.

clrd = (
    cl.load_sample("clrd")
    .groupby("LOB")
    .sum()
    .loc["wkcomp", ["CumPaidLoss", "EarnedPremNet"]]
)

cl.Chainladder().fit(clrd["CumPaidLoss"]).ultimate_ == cl.MackChainladder().fit(
    clrd["CumPaidLoss"]
).ultimate_

True

Let’s create a Mack’s Chainladder model.

mack = cl.MackChainladder().fit(clrd["CumPaidLoss"])

MackChainladder has the following additional fitted features that the deterministic Chainladder does not:

  • full_std_err_: The full standard error

  • total_process_risk_: The total process error

  • total_parameter_risk_: The total parameter error

  • mack_std_err_: The total prediction error by origin period

  • total_mack_std_err_: The total prediction error across all origin periods

Notice these are all measures of uncertainty, but where can they be applied? Let’s start by examining the link_ratios underlying the triangle between age 12 and 24.

clrd_first_lags = clrd[clrd.development <= 24][clrd.origin < "1997"]["CumPaidLoss"]
clrd_first_lags
12 24
1988 285,804 638,532
1989 307,720 684,140
1990 320,124 757,479
1991 347,417 793,749
1992 342,982 781,402
1993 342,385 743,433
1994 351,060 750,392
1995 343,841 768,575
1996 381,484 736,040

A simple average link-ratio can be directly computed.

clrd_first_lags.link_ratio.to_frame(origin_as_datetime=True).mean()[0]

/tmp/ipykernel_3244/1055289506.py:1: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  clrd_first_lags.link_ratio.to_frame(origin_as_datetime=True).mean()[0]

2.2066789527531494

We can also verify that the result is the same as the Development object.

cl.Development(average="simple").fit(clrd["CumPaidLoss"]).ldf_.to_frame(
    origin_as_datetime=False
).values[0, 0]

2.2066789527531494

The Linear Regression Framework#

Mack noted that the estimate for the LDF is really just a linear regression fit. In the case of using the simple average, it is a weighted regression where the weight is $\left (\frac{1}{X} \right )^{2}$.

Let’s take a look at the fitted coefficient and verify that this ties to the direct calculations that we made earlier. With the regression framework in hand, we can get more information about our LDF estimate than just the coefficient.

y = clrd_first_lags.to_frame(origin_as_datetime=True).values[:, 1]
x = clrd_first_lags.to_frame(origin_as_datetime=True).values[:, 0]

model = sm.WLS(y, x, weights=(1 / x) ** 2)
results = model.fit()
results.summary()

/home/docs/checkouts/readthedocs.org/user_builds/chainladder-python/conda/latest/lib/python3.11/site-packages/scipy/stats/_stats_py.py:1806: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=9
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "
WLS Regression Results
Dep. Variable: y R-squared (uncentered): 0.997
Model: WLS Adj. R-squared (uncentered): 0.997
Method: Least Squares F-statistic: 2887.
Date: Tue, 30 Jan 2024 Prob (F-statistic): 1.60e-11
Time: 16:29:27 Log-Likelihood: -107.89
No. Observations: 9 AIC: 217.8
Df Residuals: 8 BIC: 218.0
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
x1 2.2067 0.041 53.735 0.000 2.112 2.301
Omnibus: 7.448 Durbin-Watson: 1.177
Prob(Omnibus): 0.024 Jarque-Bera (JB): 2.533
Skew: -1.187 Prob(JB): 0.282
Kurtosis: 4.058 Cond. No. 1.00


Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

By toggling the weights of our regression, we can handle the most common types of averaging used in picking loss development factors.

  • For simple average, the weights are $\left (\frac{1}{X} \right )^{2}$

  • For volume-weighted average, the weights are $\left (\frac{1}{X} \right )$

  • For “regression” average, the weights are 1

print("Simple average:")
print(
    round(
        cl.Development(average="simple")
        .fit(clrd_first_lags)
        .ldf_.to_frame(origin_as_datetime=False)
        .values[0, 0],
        10,
    )
    == round(sm.WLS(y, x, weights=(1 / x) ** 2).fit().params[0], 10)
)

print("Volume-weighted average:")
print(
    round(
        cl.Development(average="volume")
        .fit(clrd_first_lags)
        .ldf_.to_frame(origin_as_datetime=False)
        .values[0, 0],
        10,
    )
    == round(sm.WLS(y, x, weights=(1 / x)).fit().params[0], 10)
)

print("Regression average:")
print(
    round(
        cl.Development(average="regression")
        .fit(clrd_first_lags)
        .ldf_.to_frame(origin_as_datetime=False)
        .values[0, 0],
        10,
    )
    == round(sm.OLS(y, x).fit().params[0], 10)
)

Simple average:
True
Volume-weighted average:
True
Regression average:
True

The regression framework is what the Development estimator uses to set development patterns. Although we discard the information in the deterministic methods, in the stochastic methods, Development has two useful statistics for estimating reserve variability, both of which come from the regression framework. The stastics are sigma_ and std_err_ , and they are used by the MackChainladder estimator to determine the prediction error of our reserves.

dev = cl.Development(average="simple").fit(clrd["CumPaidLoss"])

dev.sigma_
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
(All) 0.1232 0.0340 0.0135 0.0091 0.0074 0.0067 0.0073 0.0097 0.0032 
dev.std_err_
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
(All) 0.0411 0.0120 0.0051 0.0037 0.0033 0.0033 0.0042 0.0068 0.0032

Remember that std_err_ is calculated as $\frac{\sigma}{\sqrt{N}}$.

np.round(
    dev.sigma_.to_frame(origin_as_datetime=False).transpose()["(All)"].values
    / np.sqrt(
        clrd["CumPaidLoss"].age_to_age.to_frame(origin_as_datetime=False).count()
    ).values,
    4,
)

array([0.0411, 0.012 , 0.0051, 0.0037, 0.0033, 0.0033, 0.0042, 0.0068,
       0.0032])

Since the regression framework uses the weighting method, we can easily turn “on and off” any observation we want using the dropping capabilities such as drop_valuation in the Development estimator. Dropping link ratios not only affects the ldf_ and cdf_, but also the std_err_ and sigma of the estimates.

Can we eliminate the 1988 valuation from our triangle, which is identical to eliminating the first observation from our 12-24 regression fit? Let’s calculate the std_err for the ldf_ of ages 12-24, and compare it to the value calculated using the weighted least squares regression.

clrd["CumPaidLoss"]
12 24 36 48 60 72 84 96 108 120
1988 285,804 638,532 865,100 996,363 1,084,351 1,133,188 1,169,749 1,196,917 1,229,203 1,241,715
1989 307,720 684,140 916,996 1,065,674 1,154,072 1,210,479 1,249,886 1,291,512 1,308,706
1990 320,124 757,479 1,017,144 1,169,014 1,258,975 1,315,368 1,368,374 1,394,675
1991 347,417 793,749 1,053,414 1,209,556 1,307,164 1,381,645 1,414,747
1992 342,982 781,402 1,014,982 1,172,915 1,281,864 1,328,801
1993 342,385 743,433 959,147 1,113,314 1,187,581
1994 351,060 750,392 993,751 1,114,842
1995 343,841 768,575 962,081
1996 381,484 736,040
1997 340,132 
round(
    cl.Development(average="volume", drop_valuation="1988")
    .fit(clrd["CumPaidLoss"])
    .std_err_.to_frame(origin_as_datetime=False)
    .values[0, 0],
    8,
) == round(sm.WLS(y[1:], x[1:], weights=(1 / x[1:])).fit().bse[0], 8)

True

With sigma_ and std_err_ in hand, Mack goes on to develop recursive formulas to estimate parameter_risk_ and process_risk_.

mack.parameter_risk_
12 24 36 48 60 72 84 96 108 120 9999
1988 0 0 0 0 0 0 0 0 0 0 0
1989 0 0 0 0 0 0 0 0 0 5,251 5,251
1990 0 0 0 0 0 0 0 0 9,520 11,183 11,183
1991 0 0 0 0 0 0 0 5,984 11,629 13,161 13,161
1992 0 0 0 0 0 0 4,588 7,468 12,252 13,648 13,648
1993 0 0 0 0 0 4,037 5,981 8,187 12,259 13,502 13,502
1994 0 0 0 0 4,163 5,980 7,555 9,503 13,302 14,506 14,506
1995 0 0 0 4,921 6,736 8,137 9,446 11,118 14,502 15,620 15,620
1996 0 0 8,824 11,289 12,895 14,101 15,190 16,513 19,141 20,090 20,090
1997 0 14,499 21,075 24,749 27,093 28,657 29,907 31,164 33,103 33,897 33,897 
mack.process_risk_
12 24 36 48 60 72 84 96 108 120 9999
1988 0 0 0 0 0 0 0 0 0 0 0
1989 0 0 0 0 0 0 0 0 0 5,089 5,089
1990 0 0 0 0 0 0 0 0 12,716 13,898 13,898
1991 0 0 0 0 0 0 0 9,791 16,366 17,396 17,396
1992 0 0 0 0 0 0 8,935 13,298 18,626 19,555 19,555
1993 0 0 0 0 0 9,138 12,792 16,090 20,536 21,375 21,375
1994 0 0 0 0 10,225 14,116 16,973 19,773 23,695 24,492 24,492
1995 0 0 0 13,102 17,449 20,434 22,804 25,180 28,514 29,264 29,264
1996 0 0 25,020 31,626 35,692 38,468 40,646 42,711 45,298 46,052 46,052
1997 0 43,224 62,195 72,725 79,313 83,518 86,649 89,327 91,962 93,045 93,045

Assumption of Independence#

The Mack model makes a lot of assumptions about independence (i.e. the covariance between random processes is 0). This means that many of the Variance estimates in the MackChainladder model follow the form of $Var(A+B) = Var(A)+Var(B)$.

First, mack_std_err_2 $=$ parameter_risk_2 $+$ process_risk_2, the parameter risk and process risk is assumed to be independent.

mack.parameter_risk_**2 + mack.process_risk_**2
12 24 36 48 60 72 84 96 108 120 9999
1988
1989 53,474,629 53,474,629
1990 252,315,077 318,202,202 318,202,202
1991 131,677,828 403,094,112 475,836,802 475,836,802
1992 100,880,179 232,603,431 497,040,939 568,692,440 568,692,440
1993 99,801,841 199,401,152 325,904,005 572,006,803 639,209,994 639,209,994
1994 121,874,576 235,033,680 345,157,930 481,280,614 738,380,263 810,270,433 810,270,433
1995 195,879,863 349,828,815 483,758,514 609,246,045 757,631,482 1,023,325,766 1,100,370,499 1,100,370,499
1996 703,858,058 1,127,626,904 1,440,168,352 1,678,591,828 1,882,843,800 2,096,883,925 2,418,319,374 2,524,434,510 2,524,434,510
1997 2,078,583,588 4,312,427,152 5,901,421,925 7,024,556,506 7,796,506,775 8,402,465,469 8,950,516,203 9,552,739,954 9,806,329,251 9,806,329,251 
mack.mack_std_err_**2
12 24 36 48 60 72 84 96 108 120 9999
1988 0 0 0 0 0 0 0 0 0 0 0
1989 0 0 0 0 0 0 0 0 0 53,474,629 53,474,629
1990 0 0 0 0 0 0 0 0 252,315,077 318,202,202 318,202,202
1991 0 0 0 0 0 0 0 131,677,828 403,094,112 475,836,802 475,836,802
1992 0 0 0 0 0 0 100,880,179 232,603,431 497,040,939 568,692,440 568,692,440
1993 0 0 0 0 0 99,801,841 199,401,152 325,904,005 572,006,803 639,209,994 639,209,994
1994 0 0 0 0 121,874,576 235,033,680 345,157,930 481,280,614 738,380,263 810,270,433 810,270,433
1995 0 0 0 195,879,863 349,828,815 483,758,514 609,246,045 757,631,482 1,023,325,766 1,100,370,499 1,100,370,499
1996 0 0 703,858,058 1,127,626,904 1,440,168,352 1,678,591,828 1,882,843,800 2,096,883,925 2,418,319,374 2,524,434,510 2,524,434,510
1997 0 2,078,583,588 4,312,427,152 5,901,421,925 7,024,556,506 7,796,506,775 8,402,465,469 8,950,516,203 9,552,739,954 9,806,329,251 9,806,329,251

Second, total_process_risk_ 2 $= \sum_{origin} $ process_risk_ 2, the process risk is assumed to be independent between origins.

mack.total_process_risk_**2
12 24 36 48 60 72 84 96 108 120 9999
1988 0 1,868,353,581 4,494,250,661 6,460,788,043 7,973,402,703 9,155,354,146 10,211,709,420 11,360,087,730 13,081,563,688 13,595,400,487 13,595,400,487 
(mack.process_risk_**2).sum(axis="origin")
12 24 36 48 60 72 84 96 108 120 9999
1988 1,868,353,581 4,494,250,661 6,460,788,043 7,973,402,703 9,155,354,146 10,211,709,420 11,360,087,730 13,081,563,688 13,595,400,487 13,595,400,487

Lastly, independence is also assumed to apply to the overall standard error of reserves, as expected.

(mack.parameter_risk_**2 + mack.process_risk_**2).sum(axis=2).sum(axis=3)

106117274249.93411

(mack.mack_std_err_**2).sum(axis=2).sum(axis=3)

106117274249.93411

This over-reliance on independence is one of the weaknesses of the MackChainladder method. Nevertheless, if the data align with this assumption, then total_mack_std_err_ is a reasonable esimator of reserve variability.

Mack Reserve Variability#

The mack_std_err_ at ultimate is the reserve variability for each origin period.

mack.mack_std_err_[
    mack.mack_std_err_.development == mack.mack_std_err_.development.max()
]
9999
1988
1989 7,313
1990 17,838
1991 21,814
1992 23,847
1993 25,283
1994 28,465
1995 33,172
1996 50,244
1997 99,027

With the summary_ method, we can more easily look at the result of the MackChainladder model.

mack.summary_
Latest IBNR Ultimate Mack Std Err
1988 1,241,715 1,241,715
1989 1,308,706 13,321 1,322,027 7,313
1990 1,394,675 42,210 1,436,885 17,838
1991 1,414,747 79,409 1,494,156 21,814
1992 1,328,801 119,709 1,448,510 23,847
1993 1,187,581 167,192 1,354,773 25,283
1994 1,114,842 260,401 1,375,243 28,465
1995 962,081 402,403 1,364,484 33,172
1996 736,040 636,834 1,372,874 50,244
1997 340,132 1,056,335 1,396,467 99,027

Let’s visualize the paid to date, the estimated reserves, and their standard errors with a histogram.

plt.bar(
    mack.summary_.to_frame(origin_as_datetime=True).index.year,
    mack.summary_.to_frame(origin_as_datetime=True)["Latest"],
    label="Paid",
)
plt.bar(
    mack.summary_.to_frame(origin_as_datetime=True).index.year,
    mack.summary_.to_frame(origin_as_datetime=True)["IBNR"],
    bottom=mack.summary_.to_frame(origin_as_datetime=True)["Latest"],
    yerr=mack.summary_.to_frame(origin_as_datetime=True)["Mack Std Err"],
    label="Reserves",
)
plt.legend(loc="upper left")
plt.ylim(0, 1800000)

(0.0, 1800000.0)
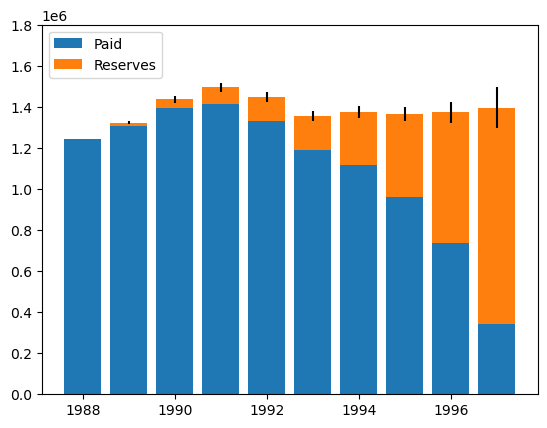
../../_images/a2bbc74ad137208df772bced4ff6a0fd2b9a3a8dcbc4437a9a366c3578c18472.png

We can also simulate the (assumed) normally distributed IBNR with np.random.normal().

ibnr_mean = mack.ibnr_.sum()
ibnr_sd = mack.total_mack_std_err_.values[0, 0]
n_trials = 10000

np.random.seed(2021)
dist = np.random.normal(ibnr_mean, ibnr_sd, size=n_trials)

plt.hist(dist, bins=50)

(array([  1.,   2.,   8.,   7.,  13.,  17.,  30.,  29.,  41.,  72.,  66.,
         94., 142., 185., 195., 274., 312., 351., 392., 419., 509., 491.,
        546., 540., 577., 537., 534., 524., 483., 448., 401., 348., 300.,
        268., 210., 163., 118.,  94.,  68.,  59.,  41.,  25.,  19.,  18.,
          7.,   5.,   3.,   5.,   5.,   4.]),
 array([2209836.99059939, 2233093.4303693 , 2256349.87013921,
        2279606.30990912, 2302862.74967904, 2326119.18944895,
        2349375.62921886, 2372632.06898877, 2395888.50875869,
        2419144.9485286 , 2442401.38829851, 2465657.82806842,
        2488914.26783834, 2512170.70760825, 2535427.14737816,
        2558683.58714807, 2581940.02691799, 2605196.4666879 ,
        2628452.90645781, 2651709.34622773, 2674965.78599764,
        2698222.22576755, 2721478.66553746, 2744735.10530738,
        2767991.54507729, 2791247.9848472 , 2814504.42461711,
        2837760.86438702, 2861017.30415694, 2884273.74392685,
        2907530.18369676, 2930786.62346667, 2954043.06323659,
        2977299.5030065 , 3000555.94277641, 3023812.38254632,
        3047068.82231624, 3070325.26208615, 3093581.70185606,
        3116838.14162597, 3140094.58139589, 3163351.0211658 ,
        3186607.46093571, 3209863.90070562, 3233120.34047554,
        3256376.78024545, 3279633.22001536, 3302889.65978527,
        3326146.09955519, 3349402.5393251 , 3372658.97909501]),
 <BarContainer object of 50 artists>)
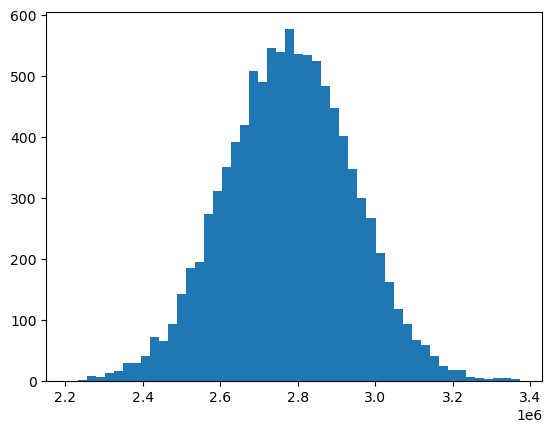
../../_images/133208ddbbfba749350b082cfd8e2544eacaf68ae69fb481a454630535d5af71.png

ODP Bootstrap Model#

The MackChainladder focuses on a regression framework for determining the variability of reserve estimates. An alternative approach is to use the statistical bootstrapping, or sampling from a triangle with replacement to simulate new triangles.

Bootstrapping imposes less model constraints than the MackChainladder, which allows for greater applicability in different scenarios. Sampling new triangles can be accomplished through the BootstrapODPSample estimator. This estimator will take a single triangle and simulate new ones from it. To simulate new triangles randomly from an existing triangle, we specify n_sims with how many triangles we want to simulate, and access the resampled_triangles_ attribute to get the simulated triangles. Notice that the shape of resampled_triangles_ matches n_sims at the first index.

samples = (
    cl.BootstrapODPSample(n_sims=10000).fit(clrd["CumPaidLoss"]).resampled_triangles_
)
samples
Triangle Summary
Valuation: 1997-12
Grain: OYDY
Shape: (10000, 1, 10, 10)
Index: [LOB]
Columns: [CumPaidLoss]

Alternatively, we could use BootstrapODPSample to transform our triangle into a resampled set.

The notion of the ODP Bootstrap is that as our simulations approach infinity, we should expect our mean simulation to converge on the basic Chainladder estimate of of reserves.

Let’s apply the basic chainladder to our original triangle and also to our simulated triangles to see whether this holds true.

ibnr_cl = cl.Chainladder().fit(clrd["CumPaidLoss"]).ibnr_.sum()
ibnr_bootstrap = cl.Chainladder().fit(samples).ibnr_.sum("origin").mean()

print(
    "Chainladder's IBNR estimate:",
    ibnr_cl,
)
print(
    "BootstrapODPSample's mean IBNR estimate:",
    ibnr_bootstrap,
)
print("Difference $:", ibnr_cl - ibnr_bootstrap)
print("Difference %:", abs(ibnr_cl - ibnr_bootstrap) / ibnr_cl)

Chainladder's IBNR estimate: 2777812.6890986315
BootstrapODPSample's mean IBNR estimate: 2777494.70036822
Difference $: 317.9887304115109
Difference %: 0.00011447450422393118

Using Deterministic Methods with Bootstrapped Samples#

Our samples is just another triangle object with all the functionality of a regular triangle. This means we can apply any functionality we want to our samples including any deterministic methods we learned about previously.

pipe = cl.Pipeline(
    steps=[("dev", cl.Development(average="simple")), ("tail", cl.TailConstant(1.05))]
)

pipe.fit(samples)

Pipeline(steps=[('dev', Development(average='simple')),
                ('tail', TailConstant(tail=1.05))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Now instead of a single ldf_ (and cdf_) array across developmental ages, we have 10,000 arrays of ldf_ (and cdf_).

pipe.named_steps.dev.ldf_.iloc[0]
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
(All) 2.0994 1.3097 1.1561 1.0788 1.0479 1.0336 1.0205 1.0065 1.0108 
pipe.named_steps.dev.ldf_.iloc[1]
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
(All) 2.2037 1.3282 1.1488 1.0842 1.0441 1.0326 1.0252 1.0230 1.0133 
pipe.named_steps.dev.ldf_.iloc[9999]
12-24 24-36 36-48 48-60 60-72 72-84 84-96 96-108 108-120
(All) 2.2571 1.3184 1.1424 1.0802 1.0490 1.0287 1.0298 1.0202 1.0072

This allows us to look at the varibility of any fitted property used. Let’s look at the distribution of the age-to-age factor between age 12 and 24, and compare it against the LDF calculated from the non-bootstrapped triangle.

resampled_ldf = pipe.named_steps.dev.ldf_
plt.hist(pipe.named_steps.dev.ldf_.values[:, 0, 0, 0], bins=50)

orig_dev = cl.Development(average="simple").fit(clrd["CumPaidLoss"])
plt.axvline(orig_dev.ldf_.values[0, 0, 0, 0], color="black", linestyle="dashed")

<matplotlib.lines.Line2D at 0x7f3c200cbf10>
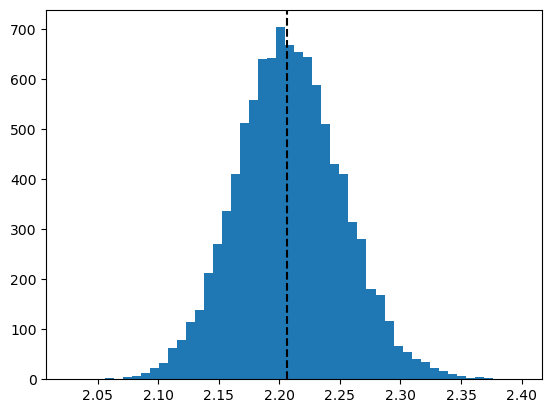
../../_images/d7fa467ca748f9c388922636614926d2ee7546e75eb3af061d051222c421f9cc.png

Bootstrap vs Mack#

We can approximate some of the Mack’s parameters calculated using the regression framework.

bootstrap_vs_mack = resampled_ldf.std("index").to_frame(origin_as_datetime=False).T
bootstrap_vs_mack.rename(columns={"(All)": "Std_Bootstrap"}, inplace=True)
bootstrap_vs_mack = bootstrap_vs_mack.merge(
    orig_dev.std_err_.to_frame(origin_as_datetime=False).T,
    left_index=True,
    right_index=True,
)
bootstrap_vs_mack.rename(columns={"(All)": "Std_Mack"}, inplace=True)

bootstrap_vs_mack
Std_Bootstrap Std_Mack
12-24 0.043550 0.041066
24-36 0.012341 0.012024
36-48 0.007317 0.005101
48-60 0.005264 0.003734
60-72 0.004043 0.003303
72-84 0.003679 0.003337
84-96 0.003723 0.004190
96-108 0.004093 0.006831
108-120 0.004150 0.003222 
width = 0.3
ages = np.arange(len(bootstrap_vs_mack))

plt.bar(
    ages - width / 2,
    bootstrap_vs_mack["Std_Bootstrap"],
    width=width,
    label="Bootstrap",
)
plt.bar(ages + width / 2, bootstrap_vs_mack["Std_Mack"], width=width, label="Mack")
plt.legend(loc="upper right")
plt.xticks(ages, bootstrap_vs_mack.index)

([<matplotlib.axis.XTick at 0x7f3c201ce450>,
  <matplotlib.axis.XTick at 0x7f3c201cee90>,
  <matplotlib.axis.XTick at 0x7f3c20d56250>,
  <matplotlib.axis.XTick at 0x7f3c20221290>,
  <matplotlib.axis.XTick at 0x7f3c202234d0>,
  <matplotlib.axis.XTick at 0x7f3c20228bd0>,
  <matplotlib.axis.XTick at 0x7f3c2022afd0>,
  <matplotlib.axis.XTick at 0x7f3c20231150>,
  <matplotlib.axis.XTick at 0x7f3c20233310>],
 [Text(0, 0, '12-24'),
  Text(1, 0, '24-36'),
  Text(2, 0, '36-48'),
  Text(3, 0, '48-60'),
  Text(4, 0, '60-72'),
  Text(5, 0, '72-84'),
  Text(6, 0, '84-96'),
  Text(7, 0, '96-108'),
  Text(8, 0, '108-120')])
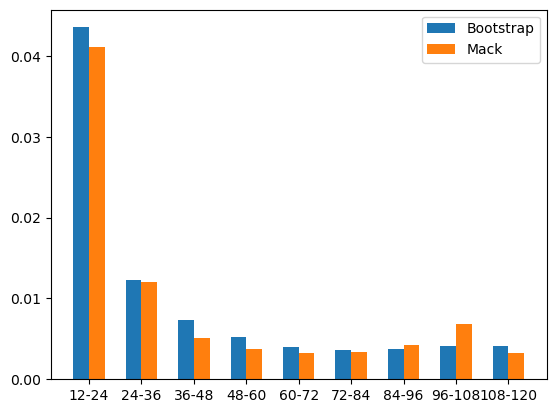
../../_images/092bcbeb563f158a85fe3a4247d0e80fa96c8206c3415e4b6cd7501c6134dd0e.png

While the MackChainladder produces statistics about the mean and variance of reserve estimates, the variance or precentile of reserves would need to be fited using maximum likelihood estimation or method of moments. However, for BootstrapODPSample based fits, we can use the empirical distribution from the samples directly to get information about variance or the precentile of the IBNR reserves.

ibnr = cl.Chainladder().fit(samples).ibnr_.sum("origin")

ibnr_std = ibnr.std()
print("Standard deviation of reserve estimate: " + f"{round(ibnr_std,0):,}")
ibnr_99 = ibnr.quantile(q=0.99)
print("99th percentile of reserve estimate: " + f"{round(ibnr_99,0):,}")

Standard deviation of reserve estimate: 138,023.0
99th percentile of reserve estimate: 3,094,916.0

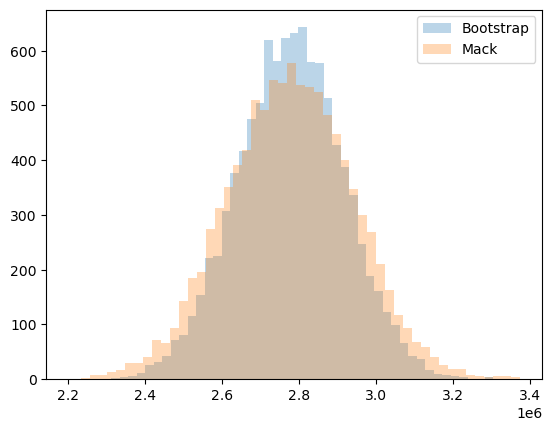
Let’s see how the MackChainladder reserve distribution compares to the BootstrapODPSample reserve distribution.

plt.hist(ibnr.to_frame(origin_as_datetime=True), bins=50, label="Bootstrap", alpha=0.3)
plt.hist(dist, bins=50, label="Mack", alpha=0.3)
plt.legend(loc="upper right")

<matplotlib.legend.Legend at 0x7f3c20267d10>
../../_images/d470bcec0bad251642199ba2c8e6a685ee6ad515949ffe212975270686fe9879.png

Expected Loss Methods with Bootstrap#

So far, we’ve only applied the multiplicative methods (i.e. basic chainladder) in a stochastic context. It is possible to use an expected loss method like the BornhuetterFerguson method does.

To do this, we will need an exposure vector.

sample_weight = clrd["EarnedPremNet"].latest_diagonal

Passing an apriori_sigma to the BornhuetterFerguson estimator tells it to consider the apriori selection itself as a random variable. Fitting a stochastic BornhuetterFerguson looks very much like the determinsitic version.

# Fit Bornhuetter-Ferguson to stochastically generated data
bf = cl.BornhuetterFerguson(0.65, apriori_sigma=0.10)
bf.fit(samples, sample_weight=sample_weight)

BornhuetterFerguson(apriori=0.65, apriori_sigma=0.1)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can use our knowledge of Triangle manipulation to grab most things we would want out of our model.

# Grab completed triangle replacing simulated known data with actual known data
full_triangle = bf.full_triangle_ - bf.X_ + clrd["CumPaidLoss"]
# Limiting to the current year for plotting
current_year = (
    full_triangle[full_triangle.origin == full_triangle.origin.max()]
    .to_frame(origin_as_datetime=True)
    .T
)

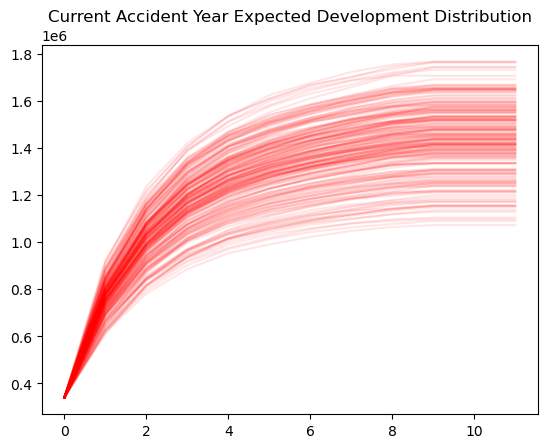
As expected, plotting the expected development of our full triangle over time from the Bootstrap BornhuetterFerguson model fans out to greater uncertainty the farther we get from our valuation date.

# Plot the data
current_year.iloc[:, :200].reset_index(drop=True).plot(
    color="red",
    legend=False,
    alpha=0.1,
    title="Current Accident Year Expected Development Distribution",
)

<Axes: title={'center': 'Current Accident Year Expected Development Distribution'}>
../../_images/45bd80a0b00503ea5f9ef021d34e8f0608bd413700cdc5611db186619b5b748a.png

Recap#

  • The Mack method approaches stochastic reserving from a regression point of view

  • Bootstrap methods approach stochastic reserving from a simulation point of view

  • Where they assumptions of each model are not violated, they produce resonably consistent estimates of reserve variability

  • Mack does impose more assumptions (i.e. constraints) on the reserve estimate making the Bootstrap approach more suitable in a broader set of applciations

  • Both methods converge to their corresponding deterministic point estimates

Contents