Tuning Development Patterns

import chainladder as cl
import pandas as pd

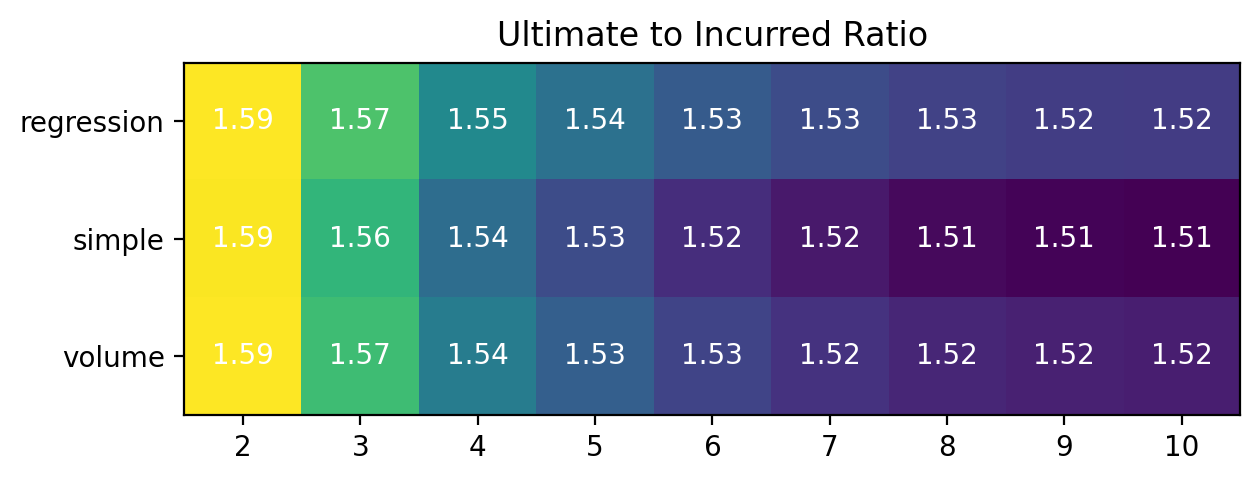
This example demonstrates testing multiple number of periods and averages in the development transformer to see its influence on the overall ultimate estimate.

tri = cl.load_sample('abc')

# Set up Pipeline
pipe = cl.Pipeline(steps=[
    ('dev',cl.Development()),
    ('chainladder',cl.Chainladder())])

# Develop scoring function that returns an Ultimate/Incurred Ratio

# Set up a GridSearch space
grid = cl.GridSearch(
    estimator=pipe,
    param_grid=dict(
        dev__n_periods=[item for item in range(2,11)],
        dev__average=['simple', 'volume', 'regression']),
    scoring=lambda x: (
        x.named_steps.chainladder.ultimate_.sum() /
        tri.latest_diagonal.sum()))
grid.fit(tri)

# Plot data
results = pd.pivot_table(grid.results_, index='dev__n_periods',
                         columns='dev__average', values='score')

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'

fig, ax = plt.subplots()
im = ax.imshow(results.T)
ax.set_yticks(np.arange(len(results.columns)))
ax.set_xticks(np.arange(len(results.index)))
ax.set_yticklabels(results.columns)
ax.set_xticklabels(results.index)
for i in range(len(results.index)):
    for j in range(len(results.columns)):
        text = ax.text(i, j, results.round(2).values[i, j],
                       ha="center", va="center", color="w")
ax.set_title("Ultimate to Incurred Ratio")
fig.tight_layout()
plt.show()